2장 Sinusoids (1)_사인파 (사인, 코사인) / 사인함수와 코사인함수/ 음성파형의 예 / 음성 신호 : BAT / 파형의 디지털화 / 주기에 대한 빈도의 관계 /

Sinusoids

• A general class of signals called cosine or sine signals.
• Write the general formula for a “sinusoidal” waveform or signal.
• From the formula, plot the sinusoid versus time.
• The most basic signals in the theory of signals and systems.
• Waveform is a SINUSOIDAL SIGNAL.
• Computer plot looks like a sine wave
• The mathematical formula: $x(t) =$ $Acos(2\pi (440)t+\varphi)$

수학 공식 : x(t) = //0을 기준으로 진동할 때 0부터 최고점까지의 거리를 알 수 있음

• Sampling rate of 5563.6 samples/sec.

코사인 신호 또는 사인 신호라고 하는 일반적인 신호 종류
사인파 파형 또는 신호에 대한 일반적인 공식을 기록함.
공식에서 사인파 대 시간 그림 표시
신호 및 시스템 이론에서 가장 기본적인 신호
파형은 사인파 신호임.
컴퓨터 플롯이 사인파처럼 보입니다

---

TUNING FORK A-440 Waveform

$T\approx 8.15-5.85 =2.3ms $

$f = \frac {1}{T} = \frac{1000}{2.3} \approx 435Hz$

---

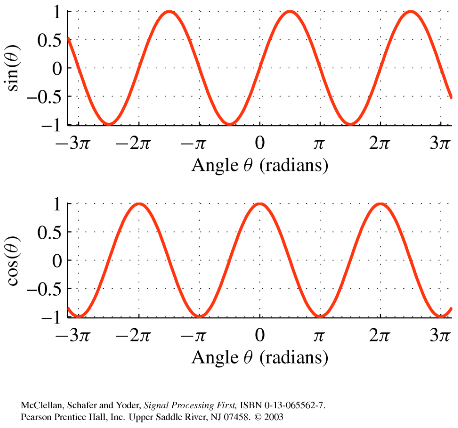
Sine and cosine function

• Sine and cosine functions plotted versus angle
  • The sine function is a cosine function that is shifted to the right by $\frac{\pi }{2}$
  • $sin\theta =cos\theta -\frac{\pi }{2}$

사인함수는 코사인 함수를 $ \frac{\pi }{2}$만큼 오른쪽으로 이동한 것임.

---

SPEECH EXAMPLE

• More complicated signal (BAT.WAV)
• Waveform x(t) is NOT a sinusoid
• Theory will tell us
  
  • x(t) is approximately a sum of sinusoids
  • FOURIER ANALYSIS
    
    • Break x(t) into its sinusoidal components
  • Called the FREQUENCY SPECTRUM

더 복잡한 신호.
파형 x(t)는 사인파가 아님
x(t)는 대략 사인파의 합임.
푸리에 급수 : x(t)를 사인파 구성요소로 분할함.
주파수 스펙트럼이라고도 부름.

---

Speech Signal : BAT

• Nearly Periodic in the vowel region
  
  • Period is (Approximately) T = 0.0065 sec.

모음영역에서 거의 주기적임 // 주기는 (약) T = 0.0065초임.

---

DIGITIZE the WAVEFORM

• x[n] is a SAMPLED SINUSOID
  
  • A list of numbers stored in memory
• Sample at 11,025 samples per second
  
  • Called the SAMPLING RATE of the A/D
  • Time between samples is
    
    • 1/11025 = 90.7 microsec.
• Output via D/A hardware (at$F_{samp}$)

x[n]는 샘플링된 사인파.
- 메모리에 저장된 숫자 목록
초당 11,025개의 샘플로 샘플링
- A/D의 샘플링 속도라고 불림.
- 샘플 간의 시간은 $\frac{1}{11025}$ = 90.7 microsec.
D/A 하드웨어를 통한 출력($F_{samp}$에서)

---

SINES and COSINES

• Always use the COSINE FORM (항상 코사인 함수가 메인)

$A(cos(2\pi(440)t+\varphi)$

• Sine is a special case :                                                   ↕

$sin(\omega t)=cos(\omega t-\frac{\pi}{2})$

---

SINUSOIDAL SIGNAL

• Computer plot looks like a sine wave

$Acos(\omega t+\varphi)$

• FREQUENCY   $\omega$
  • Radians/sec.
  • Hertz (cycles/sec)
    • $\omega = (2\pi)f$
• AMPLITUDE   $A$
  
  • Magnitude
• PERIOD (in sec.)
  • $T=\frac{1}{f}=\frac{2\pi}{\omega}$
• PHASE   $\varphi$

주파수 (빈도수) , 진폭 (크기) , 주기, 상
phase : shift advance

---

EXAMPLE of SINUSOID

$5cos(0.3\pi t+1.2\pi)$

---

PLOT COSINE SIGNAL

$5cos(0.3\pi t+1.2\pi)$

• Formula defines $A, \omega , and  \; \phi$

$A = 5$

$\omega = 0.3\pi$

$\varphi = 1.2\pi$

---

PLOTTING COSINE SIGNAL from the FORMULA

$5cos(0.3\pi t+1.2\pi)$

• Determine  period:

$T = \frac{2\pi}{\omega} = \frac{2\pi}{0.3\pi} = \frac {20}{3}$

• Determine a peak location by solving 

$(\omega t+\phi =0) \Rightarrow (0.3\pi t+1.2\pi )=0$

• Zero crossing is T/4 before or after
• Positive & Negative peaks spaced by T/2

peak location : t = -4
위 식에서 peak location은 $1.2\pi$만큼 딜레이 됨.
zero crossing(0교차) : 양수에서 음수, 음수에서 양수로 변화가 일어나는 곳
양수와 음수의 정점은 주기의 절반만큼의 차이가 남.

---

PLOT the SINUSOID

$5cos(0.3\pi t+1.2\pi)$

• Use T = 20/3 and the peak location at t=-4

주기 T = 20/3과 정점의 위치 t=-4를 이용하기

---

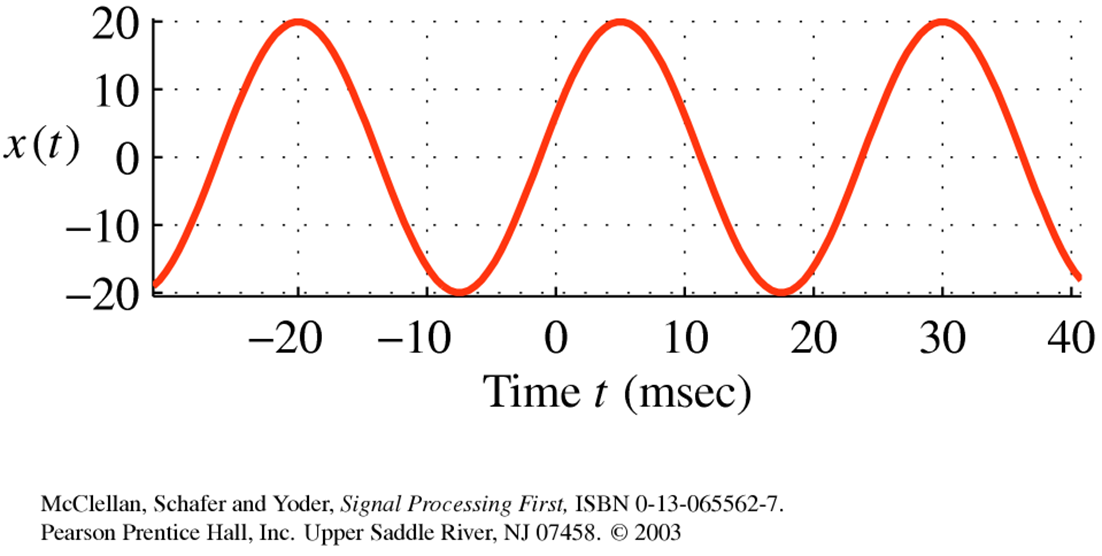
Relation of Frequency to Period

• Sinusodal sign with parameter $A = 20,\;\omega =2\pi (40),\;f=40,\;and \; \phi =-0.4\pi$

• For the higher frequency, the signal varies more rapidly with time, the cycle length is a shorter time interval.

주파수가 높을수록 신호는 시간이 지남에 따라 더 빠르게 변함.사이클 길이의 시간 간격은 더 짧아짐.