좌표계
3차원 물체의 표현
-
경계면 표현(Boundary Surface Representation)
- 메쉬(Mesh), 표면 메쉬(Surface Mesh), 다각형 메쉬(Polygon Mesh), 표면 다각형(Surface Polygon), 다각형(Polygon)
- 사각형 메쉬 (Rectangular Mesh) : 평면 보장 못함, 정확한 렌더링이 어려움
- 삼각형 메쉬 (Triangular Mesh) : 평면 보장, 메쉬 수가 2배로 늘고 드로잉 속도가 늦어짐.

-
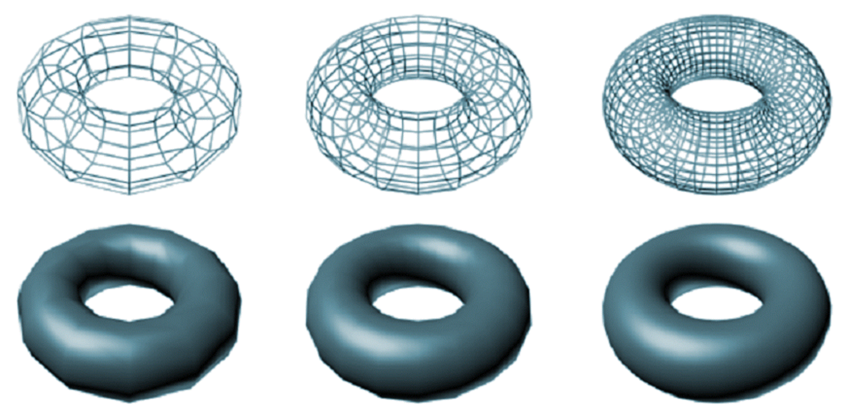
Wireframe, Solid Rendering
- 와이어 프레임 : 드로잉 속도가 빠름
- 가끔씩 솔리드 렌더링으로 외형 확인



더보기
- 3차원 물체를 표현하는 방법은 물체 표면만 표현하는 방법과 물체 내부까지 표현하는 방법이 존재함.
- 그래픽에서는 물체 표면만 표현하는 방법이 주로 사용됨. = Boundary Surface Representation : 물체면을 평면 다각형의 집합으로 나타냄.
- 곡면을 표현하기 위해 필요한 다각형의 수는 곡면의 곡률에 정비례함. 곡면을 표현하는 평면 다각형 하나하나를 Mesh 혹은 Polygon이라고 함. 표면 메쉬에 사용되는 다각형은 사각형 또는 삼각형임.
- 정밀도 : 삼각형 > 사각형 메시 → 공간상에서 임의의 네 점을 연결하여 이루어진 면은 일반적으로 평면이 아니라 휜 면이 됨. 물체면의 색상을 계산하는 렌더링 단계에서 메시 자체를 평면으로 가정한다는 점을 고려하면 사각형 메시에서 정확한 렌더링을 기대하기 어려움. 공간상의 세 점을 연결한 면은 반드시 평면
- 렌더링에는 와이어 프레임 렌더링 / 솔리드 렌더링이 있음. 와이어 프레임 렌더링은 다각형 메시의 경계선만으로 물체를 묘사하는 것, 물체의 뼈대만을 선분으로 묘사. 솔리드 렌더링은 다각형 메시에 조명을 가하여 색상이 드러난 물체를 그리는 것.
- 모델링은 결국 정점의 위치를 정의하는 것.
- 삼각형 : 사각형을 반으로 쪼개면 삼각형이므로 메쉬수가 2배로 늚. 삼각형을 사용하면 모든 알고리즘에 문제 없음
벡터 공간
-
스칼라(Scalar)
- 크기만 있고 방향은 없는 양 (기온이 10도, 나이가 20)
- 교환법칙(Commutative Law) 성립
- 결합법칙(Associative Law) 성립
- 역원법칙(Inverse Law) - 어떤 스칼라 A에 대해 항등원(Identity)이 되는 B가 반드시 존재
-
벡터(Vector)
- 크기와 방향을 동시에 지닌 것 (바람은 풍력과 풍향을 지님, 물의 흐름, 힘)
- 모든 벡터에는 역 벡터가 존재
- 스칼라를 벡터에 곱할 수 있음
- 벡터의 합은 벡터임
- 벡터 공간 (Vector Space)
- 주어진 벡터로부터 파생되는 모든 벡터의 집합을 의미함.
더보기
- 스칼라는 아무런 기하학적 특성도 없다.
- 벡터는 같은 크기의 방향만 반대로 하면 역벡터가 존재한다. 벡터에 스칼라 값을 곱하면 방향은 동일하면서, 크기가 스칼라배가되는 벡터가 정의된다. 두 벡터의 합은 두 벡터에 의해 만들어지는 평행사변형의 대각선 벡터와 동일하다.
- 주어진 벡터들에 스칼라를 곱하거나 벡터끼리의 합성에 의해 만들어지는 벡터의 집합을 벡터공간이라 한다.
어파인 공간

V = Q – P
Q = V + P
- 등식의 우변은 벡터와 점 사이의 덧셈이 됨
공간상이 위치를 중시하는 기하학에서 벡터만으로 위치를 표시하기 어려움
→ 점이라는 개념을 추가하여 위치 표시
-
어파인 공간(同族, 親密, Affine Space)
- 점과 벡터를 동족처럼 취급함으로써 벡터공간을 확장
- 어파인 연산
- 벡터와 벡터의 덧셈 (뺄셈)
- 스칼라와 벡터의 곱셈 (나눗셈)
- 점과 벡터의 덧셈 (뺄셈).
- 선분 표현 (Line Segments)

어파인 공간에서 일반적인 성분의 식
V = P + (1/2)(Q - P)
V = P + t (Q - P) = (1 - t)P + (t)Q (0 ≤ t ≤ 1)
-
어파인 공간에서 어파인 합(Affine Sum)
- 점의 계수 합이 1이 되는 경우
- 점의 덧셈은 각 점들 앞의 계수 합이 1일 때에 한해서만 허용됨
더보기
- 점 (Point) : 위치만 있고, 크기나 방향은 없다. 점이라는 개념을 벡터 공간에 추가하면, 방향뿐만 아니라 위치도 표시 가능. 벡터 사이는 물론 점과 점, 점과 벡터 사이의 연산이 허용되어야 한다.
- 어파인 공간 : 벡터 공간에 점이라는 개념을 추가해서 벡터 공간을 확장한 것이다. 3가지 연산이 가능하다. 벡터 + - 벡터, 벡터 */벡터, 점 +- 벡터.
- 공간상의 위치를 중시하는 기하학에서 벡터만으로 위치를 표시하기는 어렵다. 점이라는 개념을 추가하면 벡터 공간에 방향뿐만 아니라 위치도 표시할 수 있다.
- 점이 몇 개가 되든 각 점 앞의 계수 합이 1이 되는 경우를 어파인 합이라고 부른다
좌표축과 좌표계
-
오른손 좌표계와 왼손 좌표계
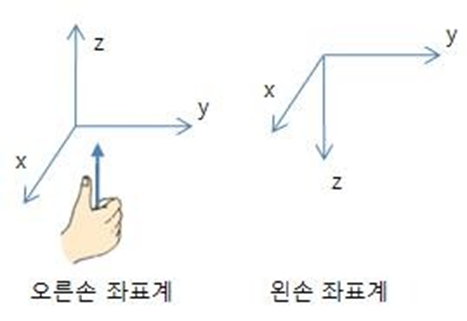
- 축 눈금 변화

-
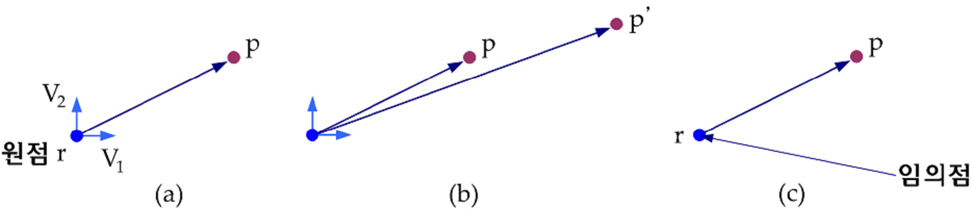
기반벡터
- 벡터 $p=4V_{1}+2V_{2}$
- 자신의 합성에 의해 다른 모든 벡터를 표시할 수 있는 벡터를 기반벡터로 함
- 기반벡터는 그들끼리 선형 독립 (Linear Independence)이어야 함.
- 공간상에 서로 직각으로 교차하는 벡터는 선형 독립임.
- 벡터 $p=4V_{1}+2V_{2}$

-
좌표계(Coordinate System)
- 원점과 기반벡터로 구성되는 프레임
3차원 좌표계 = $(r,\;V_{1},\;V_{2},\;V_{3})$ - 원점 : 어파인 공간에서 기반벡터 시작점을 일치시킨 곳
- 점 $p=r+4V_{1}+2V_{2}+V_{3}$
- 원점과 기반벡터로 구성되는 프레임
더보기
- 3차원 공간에서 물체의 위치는 주어진 좌표계(Coordinate System)를 기준으로 표시된다. (원기둥 좌표계, 원구 좌표계, 직교 좌표계 등 존재) 가장 많이 사용되는 것은 직교좌표계 (Cartesian coordinate)이다. 3차원 직교 좌표계는 원점에서 서로 직각으로 교차하는 3개의 좌표축 벡터로 이루어진다. x,y,z축의 방향은 일반적으로 오른손 법칙을 따른다. 직교 좌표계는 원점 위치, 축방향, 축 눈금의 길이 등에 의해 정의된다.
- 자신의 합성에 의해 다른 모든 벡터를 표시할 수 있는 벡터를 기반 벡터. 기반 벡터의 특징은 그들끼리 선형 독립이어야 한다는 점이다. 어떤 벡터가 다른 벡터의 선형 조합으로 표현된다면 이는 선형독립이 아니다. 다시말해 기반 벡터 관계가 아니다. 시각적으로 말하자면 공간상에 서로 직각으로 교차하는 벡터는 선형독립이다
- 점의 위치를 표현하기 위한 기반 벡터의 수가 바로 차원이다. 점의 좌표는 이러한 기반 벡터를 기준으로 나타낸 것이다. 각각 기반 벡터에 곱해지는 계수가 바로 좌표이다.
- 벡터에 점을 추가한 것이 ‘어파인 공간’이고, 어파인 공간에서는 기반 벡터를 서로 흩어 놓을 것이 아니라 시작 위치를 한 점에 고정할 필요가 생긴다. 이게 바로 ‘원점’이다.
- 3차원 정점 좌표를 나타내기 위해서는 원점과 3개의 기반 벡터를 요한다. 좌표계는 원점과 기반 벡터로 구성되는 프레임이다.
동차좌표 (Homogenous Coordinates)
-
벡터와 점의 표현이 다름
$v=4V_{1}+2V_{2}+V_{3}$
$P=r+4V_{1}+2V_{2}+V_{3}$ - 차원을 하나 올리면 동일 방법으로 표현
$v=4V_{1}+2V_{2}+V_{3}+0r=$(4, 2, 1, 0) 벡터
$P=4V_{1}+2V_{2}+V_{3}+1r=$(4, 2, 1, 1) 점 - 3차원 동차좌표
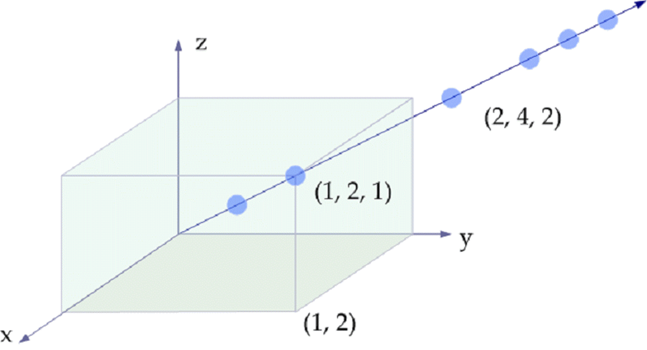
4차원 동차좌표 (x, y, z, w) → 3차원 실제좌표 (x/w, y/w, z/w) - 일반적으로 컴퓨터 그래픽에서는 동차좌표로 표시
더보기
- 벡터인지, 점인지에 따라 표현방식이 달라야 한다. 지금까지대로면 벡터v와 점 p 모두 좌표(4,2,1)인데 이러한 불편을 해소하기 위해 사용하는 것이 동차좌표이다. 3차원 좌표를 3개의 요소가 아니라 차원을 하나 올려서 4개의 요소로 표현한다. 마지막 요소가 요소가 0이면 벡터를 그렇지 않고 1이면 점을 의미하도록 한 것. 이렇게 함으로써 벡터의 점을 동일한 방법으로 표현할 수 있게 된다. 수학적으로 보면 이는 3차원에서 4차원으로의 사상(mapping)이다.
- 좌표계 차원을 n이라할때, n개로 이루어진 좌표만으로 표현못하는 요소가 있어, 이를 해결하기 위해 n+1로 표현한 좌표계를 동차좌표계라 한다. (3차원상의 점과 벡터를 3개가 아닌 4개의 요소로 표현)
- 마지막 요소가 0이면 벡터를, 1이면 점을 의미한다.
- 만약 3차원 동차좌표를 4차원(x, y, z, w)로 좌표로 표시하면, 3차원 실제 좌표는 (x/w, y/w, z/w)가 된다.
- 컴퓨터 그래픽에서는 모든 좌표를 동차 좌표로 표시한다. 3차원 그래픽 파이프라인 하드웨어는 동차 좌표 처리를 위해 한 번에 4개의 요소를 입력하고 처리할 수 있도록 설계되어있다
'전공 > 컴퓨터 그래픽스' 카테고리의 다른 글
| 모델변환과 시점변환 (3)지엘의 모델변환 (0) | 2023.04.22 |
|---|---|
| 모델변환과 시점변환 (2)기하변환 (1) | 2023.04.13 |
| OpenGL 기본 틀 : 정점배열 (1) | 2023.04.11 |
| OpenGL 기본틀 : Callback 프로그래밍 (2)Menu Callback, Idle Callback, Timer Callback (0) | 2023.04.11 |
| OpenGL 기본틀 : Callback 프로그래밍 (1)Reshape Callback, Keyboard Callback, Mouse Callback (0) | 2023.04.10 |




댓글